Доверительный интервал для дисперсии позволяет оценить диапазон, в котором с заданной вероятностью находится истинное значение дисперсии генеральной совокупности. Рассмотрим методику построения такого интервала.
Содержание
Основные понятия
- Дисперсия выборки (s²) - оценка дисперсии генеральной совокупности
- Уровень доверия (1-α) - вероятность нахождения истинного значения в интервале
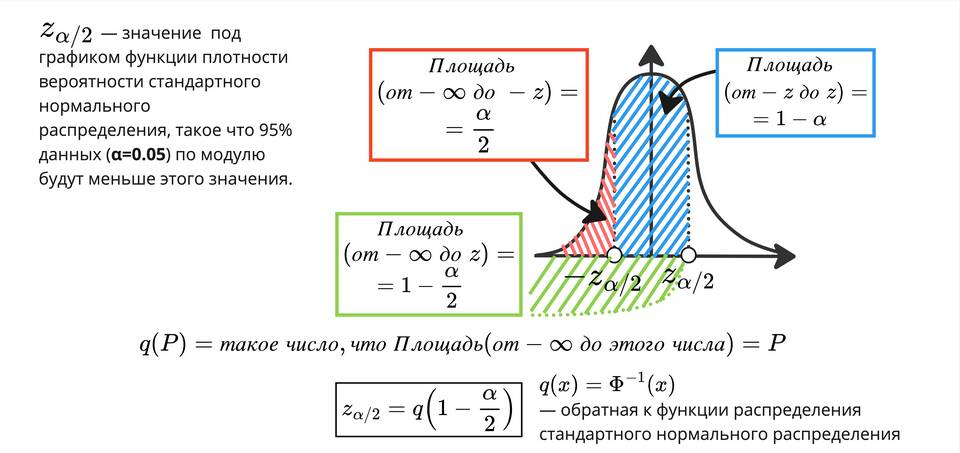
- Распределение хи-квадрат (χ²) - основа для построения интервала
Условия применения
| Условие | Описание |
| Нормальность распределения | Данные должны быть распределены нормально |
| Независимость наблюдений | Элементы выборки должны быть независимы |
| Размер выборки | Лучше работает для n > 30 |
Формула доверительного интервала
Для генеральной дисперсии σ² доверительный интервал вычисляется по формуле:
| Нижняя граница | (n-1)s² / χ²α/2,n-1 |
| Верхняя граница | (n-1)s² / χ²1-α/2,n-1 |
Пошаговый алгоритм расчета
Вычисление выборочной дисперсии
- Найдите среднее значение выборки (x̄)
- Вычислите сумму квадратов отклонений: Σ(xᵢ - x̄)²
- Разделите на (n-1) для несмещенной оценки: s² = Σ(xᵢ - x̄)² / (n-1)
Определение критических значений χ²
- Выберите уровень значимости α (обычно 0.05 или 0.01)
- Найдите χ²α/2,n-1 и χ²1-α/2,n-1 по таблице распределения
- Для n=20 и α=0.05: χ²0.025,19 = 32.85, χ²0.975,19 = 8.91
Расчет границ интервала
| Пример | Для s²=15, n=20, α=0.05 |
| Нижняя граница | (20-1)×15 / 32.85 ≈ 8.68 |
| Верхняя граница | (20-1)×15 / 8.91 ≈ 31.99 |
Интерпретация результатов
Для примера выше можно утверждать с 95% уверенностью, что истинная дисперсия генеральной совокупности находится в интервале от 8.68 до 31.99.
Особенности расчета
- Интервал асимметричен относительно s²
- Ширина интервала уменьшается с ростом n
- Для малых выборок интервал будет широким
Важные замечания
При построении доверительного интервала для стандартного отклонения (σ) необходимо извлечь квадратный корень из границ интервала для дисперсии. Для не нормальных распределений требуются другие методы, например бутстреп.